| Calendar Name | Standard Calendar of Earth |
|---|---|
| Abbreviation | SCE (Standard Calendar of Earth) |
| Worlds | Earth, Lagrangian space settlements, Lunar settlements, Bessel, Calena, Hydra Base, Lysander, Sabrina, Serenese Federation, Techbase |
| Epoch | 2301 January 1 SCE |
| Days in year | 365 or 366 |
| Average length of calendar year | 365159⁄656 (365.242378) Standard days |
| Months in year | 12 |
| Days in week | 7 |
| Perpetual calendar | No |
| Unbroken week | Yes |
| Intercalation rules | Intercalate 1 day when the remainder of (159 × Year + 522) / 656 < 159 |
| January | February | March | April | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 31 | 1 | 2 | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |||
| 22 | 23 | 24 | 25 | 26 | 27 | 28 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | |||
| 29 | 30 | 31 | 26 | 27 | 28 | 29 | 30 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 28 | 29 | 30 | |||||||||||||
| May | June | July | August | |||||||||||||||||||||||||||
| Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | |||
| 1 | 2 | 3 | 4 | 30 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | |||||||||||||||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |||
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |||
| 26 | 27 | 28 | 29 | 30 | 31 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 28 | 29 | 30 | 26 | 27 | 28 | 29 | 30 | 31 | |||||||||
| September | October | November | December | |||||||||||||||||||||||||||
| Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | Mo | Tu | We | Th | Fr | Sa | Su | |||
| 30 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 30 | 31 | 1 | |||||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |||
| 23 | 24 | 25 | 26 | 27 | 28 | 29 | 28 | 29 | 30 | 31 | 25 | 26 | 27 | 28 | 29 | 30 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | |||||||
| Month | Common years | Leap years |
|---|---|---|
| January | No change | No change |
| February | ||
| March | Count backwards two days | Count backwards one day |
| April | ||
| May | ||
| June | ||
| July | ||
| August | Count backwards one day | No change |
| September | ||
| October | ||
| November | ||
| December |
The Standard Calendar is based on the Gregorian calendar, which in turn is based on the Julian calendar and other calendars of ancient Rome. The major differences between the Standard Calendar and the Gregorian calendar are:
The advantages of the Standard Calendar are:
The Standard Calendar is used on Earth, and is also in use on most colony worlds that are tidelocked to their sun. Prometheus is the only tidelocked world that does not use the Standard Calendar.
The Standard Calendar came into effect on 2301 January 1. The standard abbreviation used for dates in this calendar is SCE (Standard Common Era or Standard Calendar of Earth). The Standard Calendar is used on the Local Space website for all dates on or after 2301 January 1.
A year is a leap year in the Standard Calendar if (Year × 159 + 522) mod 656 < 159.
This formula can also be used to find the time of the March equinox in any year to within about 15 minutes. However, 159 has to be deducted from the constant in the leap year formula because the leap year formula is based on the time of the equinox in the following year. Thus, the equinox formula has the constant 363 where the leap year formula has 522. The leap year count in the Easter formula (see below) also has the constant 363 for the same reason.
Example: Find March equinox for 2009 using the rules for the Standard Calendar.
This method of calculating Easter in the Standard Calendar abolishes the Epacts, Golden Numbers, Dominical Letters and other details that make the computation of the date of Easter more complex than it needs to be. Some complexity remains because some complexity is inevitable when dealing with the need to fit the motion of the moon to a solar calendar.
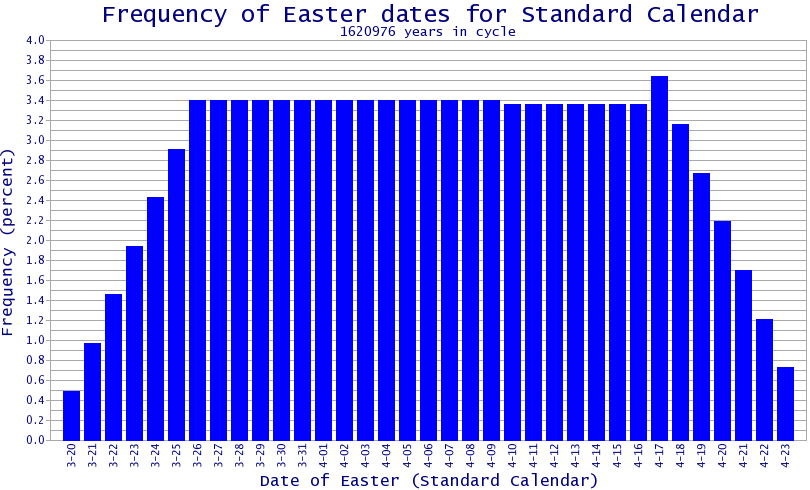
Easter can occur between March 19 and April 22 in the Standard Calendar. This date range is equivalent to March 21 to April 24 in Gregorian common years, or March 20 to April 23 in Gregorian leap years. These date ranges are slightly earlier than the nominal dates of Easter in the Gregorian calendar (March 22 to April 25). This occurs because the dates of Easter in the Standard Calendar are bound more tightly to the equinox, and are thus more accurate.
Easter in the Standard Calendar is based on a 353-year cycle, whereas the Gregorian Easter uses the 19-year Metonic cycle with periodic adjustments. The dates of the Standard Easter do not recur for 1,620,976 years (353 × 656 × 7); the Gregorian Easter has a cycle of 5,700,000 years.
 |
Easter in the Standard Calendar is calculated as follows:
// Find the date and time of the Ecclesiastical Full Moon, which is the // first full moon after the Equinox. The Equinox is assumed to fall // always on March 18 (Standard Calendar), which it does in most years // in the 24th to 30th centuries as seen from the Prime Meridian. // The first full moon cannot fall earlier than March 19 (Standard Calendar) // to minimise the chance of the full moon falling before the equinox. MoonDeterminant = (Year × 223 + 183) mod 353 // The floor() function discards the fractional part of a number. // In all cases the floor() function is used when numbers are divided. // This is equivalent to integer division where the remainders are discarded. // // 353 × 108 / 1291 is approximately equal to 29.53059644, or 29 days // 12 hours 44 minutes 3.53 seconds, which is very close to the value // for the mean lunar month, being 0.65 seconds longer than the mean lunar // month in 2000. FullMoon = floor (MoonDeterminant × 108 / 1291) // The Leap Day Count is used to calculate the number of leap days // that have occurred prior to the start of the current year, // according to the Standard Calendar. The intercalation of the // Gregorian Calendar may be substituted here, provided that the // above constants for calculating the timing of the Full Moon are // adjusted to ensure the length of the lunar month is as accurate // as possible. LeapDayCount = floor (Year × 159 + 363 / 656) // Easter must occur on the Sunday following the full moon, so determine // how many extra days are needed to make Easter fall on the following Sunday. ExtraDays = 7 − ((LeapDayCount + Year + 2 + FullMoon) mod 7) // 19 days are added because March 19 is the date of the earliest // full moon after the equinox. DateOfEaster = FullMoon + ExtraDays + 19 // If Easter would occur on April 24 (Standard Calendar), the date is // adjusted so that Easter occurs one week earlier. The Julian and // Gregorian Easters limited the range of valid dates for Easter to a // 35–day span, and this limit is maintained in the Standard Calendar. // This adjustment makes April 17 the most likely date on which Easter // can fall in the Standard Calendar. // This correction is applied about 0.243% of the time, or six times every // 2471 years on average. DateOfEaster = DateOfEaster − 7 × floor (DateOfEaster / 55) // Extract the date of Easter (Standard Calendar). // To find the equivalent Gregorian date, add 2 days to DateOfEaster // before extracting the month in common years, or 1 day in leap years. Month = floor (DateOfEaster / 32) + 3 Day = 93 + DateOfEaster − Month × 31
MoonDeterminant = (Year × 223 + 183) mod 353 // MoonDeterminant = 105 FullMoon = floor (MoonDeterminant × 108 / 1291) // FullMoon = 8 LeapDayCount = floor ((Year × 159 + 363) / 656) // LeapDayCount = 582 ExtraDays = 7 − ((LeapDayCount + Year + 2 + FullMoon) mod 7) // ExtraDays = 3 DateOfEaster = FullMoon + ExtraDays + 19 // DateOfEaster = 30 DateOfEaster = DateOfEaster − 7 × floor (DateOfEaster / 54) // DateOfEaster = 30 Month = floor (DateOfEaster / 32) + 3 // Month = 3 (March) Day = 93 + DateOfEaster − Month × 31 // Day = 30
The date of Easter in 2401 is March 30 (Standard Calendar), which is equivalent to April 1 in the Gregorian Calendar. This is the same as the Gregorian date of Easter in 2401. On average, the Standard Easter matches the date of Gregorian Easter about 90% of the time. Where the dates of Easter do not match, the Standard Calendar usually has the more accurate date.
An alternative method of determining the date of Easter fixes the date of Easter to a single week, instead of allowing it to fall in any of five weeks. This method of calculating the date of Easter is based on the moveable Easter.
In this method, Easter Sunday is the Sunday after the first Friday in April. Thus, Good Friday always falls in the first seven days of April, and Easter Sunday falls between April 3 and April 9. This corresponds to the third week of the five possible weeks that can occur with the Moveable Easter method shown above.
Fixing the date of Easter to the first week in April in this way is sound because the most likely date for the crucifixion of Jesus is Friday April 3, 33 AD, which is in the first week of April. The chosen weekend is the third weekend out of the five possible weekends for Easter.
The formula for Movable Easter can be used to find the date for Fixed Easter by assuming that the ecclesiastical full moon always falls on April 2. This cuts out most of the steps in the calculation, leaving a three-step calculation:
LeapDayCount = floor ((Year × 159 + 363) / 656)
ExtraDays = 7 − ((LeapDayCount + Year + 2) mod 7)
Day = ExtraDays + 2
This can be reduced to a one-line formula:
Day = 9 - ((floor ((Year × 159 + 363) / 656) + Year + 2) mod 7)
LeapDayCount = floor ((Year × 159 + 363) / 656) // LeapDayCount = 582 ExtraDays = 7 − ((LeapDayCount + Year + 2) mod 7) // ExtraDays = 4 Day = ExtraDays + 2 // Day = 6
As discussed above, the only years in the first millennium of the Standard Calendar (2301 to 3300) in which the March equinox is predicted to fall outside March 18 (Universal Time) when using the Leap Year algorithm of the Standard Calendar are 2696 (23:59 on March 17), 2795 (23:56 on March 17) and 2894 (00:02 on March 19). The calculations that give these results are based on VSOP87 theory and extrapolations of Delta T as described in the second edition of Astronomical Algorithms by Jean Meeus[1]. These calculations are subject to some error due to the unknown future values for Delta T, which varies irregularly and can only be determined from observation. To a lesser extent, the VSOP87 calculations are also known to have small errors. It is likely that the predicted Delta T values used may be in error, which would cause the actual times to be different to the predicted times. If the predicted times differ from the actual times by more than a few minutes, different years may be found to have equinoxes that occur on dates other than March 18, or the years given above may be found to be no longer in error.
The years between 2301 and 3500 where the March equinox is predicted to fall outside the nominal date of March 18 (Universal Time) or that is predicted to fall less than 15 minutes inside this nominal date are given in the following table. The years where the equinox is predicted to fall outside March 18 are highlighted.
| 2337-03-18 23:52:17.68 | 2597-03-18 00:14:26.81 | 2795-03-17 23:56:55.99 | 3088-03-18 00:12:30.96 |
| 2366-03-18 00:10:47.09 | 2630-03-18 00:07:59.91 | 2861-03-18 23:52:33.38 | 3319-03-18 00:14:35.61 |
| 2370-03-18 23:47:17.16 | 2663-03-18 00:03:07.96 | 2894-03-19 00:02:43.07 | 3352-03-18 00:13:34.46 |
| 2399-03-18 00:11:46.14 | 2696-03-17 23:59:28.49 | 2927-03-18 23:49:21.47 | 3385-03-18 00:11:30.65 |
| 2531-03-18 00:03:36.23 | 2729-03-18 00:02:44.90 | 3026-03-18 23:48:27.29 | 3484-03-19 00:13:00.00 |
| 2564-03-18 00:07:42.38 | 2762-03-18 00:04:32.82 | 3059-03-18 23:47:20.95 |
It is not possible to have no years in a millennium with an equinox falling outside a particular date using simple arithmetic-based rules because equinoxes and solstices may be early or late of the mean time by as much as 15 minutes due to the perturbations of the sun, moon and planets.
However, such small errors are a great improvement on the relatively large errors in the timing of the March equinox in the Gregorian calendar. The following were calculated using VSOP87 algorithms and values for Delta T given in Meeus[1].
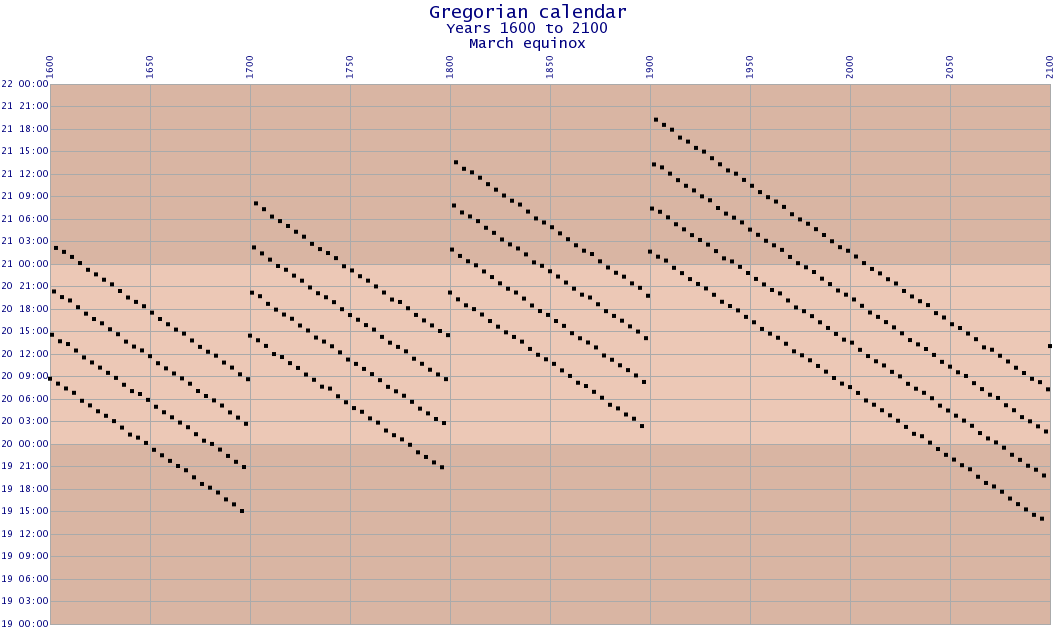
This chart shows the typical range of errors in the Gregorian calendar. The 400-year cycle of the calendar is shown, with an additional 100 years to show how the calendar wraps at the end of a cycle. The pattern of one leap year every four years produces a clear pattern of four rows of dots, corresponding to three common years and one leap year, and obvious discontinuties at the century years that are not leap years.
The earliest equinox in the range shown is March 19, 2096 at 14:02, and the latest equinox is March 21, 1903 at 19:14, a range of about 53 hours. This large range of equinox dates is much reduced in the Standard Calendar.
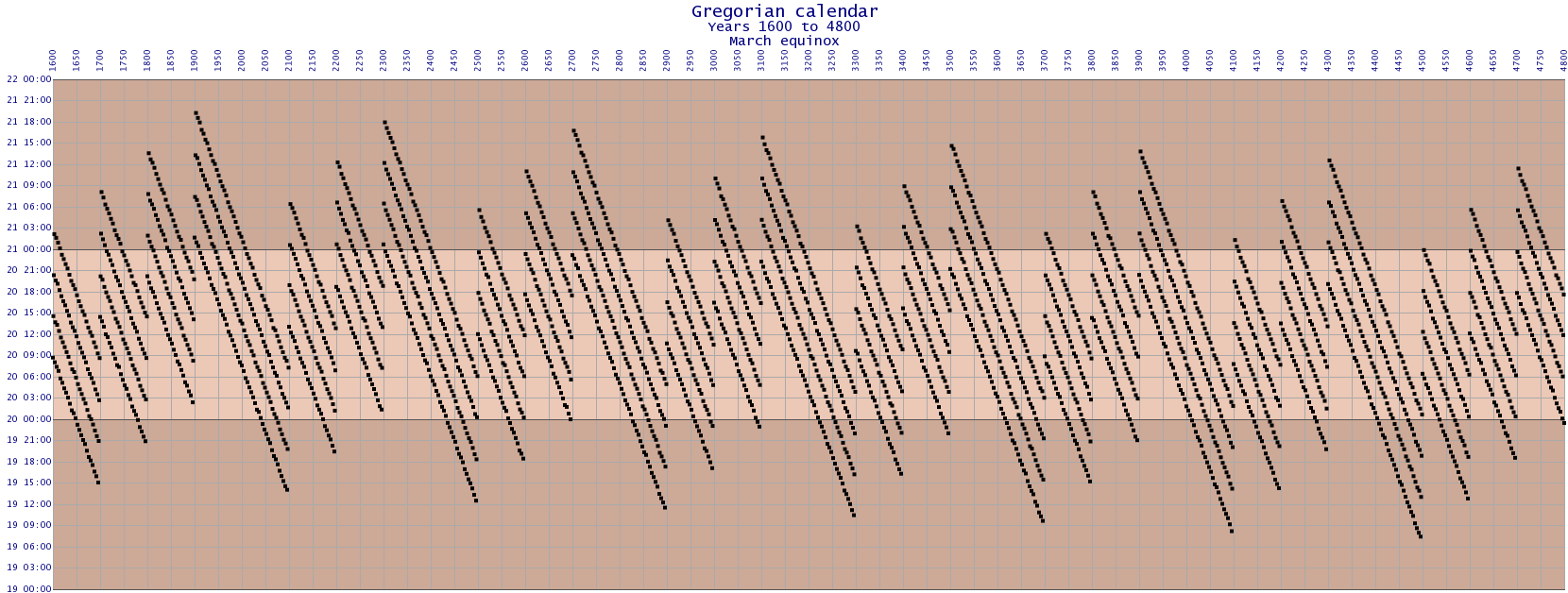
This chart also shows the errors of the Gregorian calendar, calculated for a range of 3200 years. Here, a gradual drift to earlier times is apparent. This drift is due to the Gregorian period of 365.2425 years being slightly too long for the March equinox by about nine seconds a year, or about 1 hour in 400 years. A more accurate figure for the March equinox year over this period is 365.2424 days.

When leap years are spaced more evenly, the error range is much smaller. Here, the leap years are spaced regularly with 159 leap years in 656 years, which is the ratio for the Standard Calendar from 2301.

The Standard Calendar is introduced in 2301, with a length of 365159⁄656 (365.242378) years and evenly-spaced intercalation.

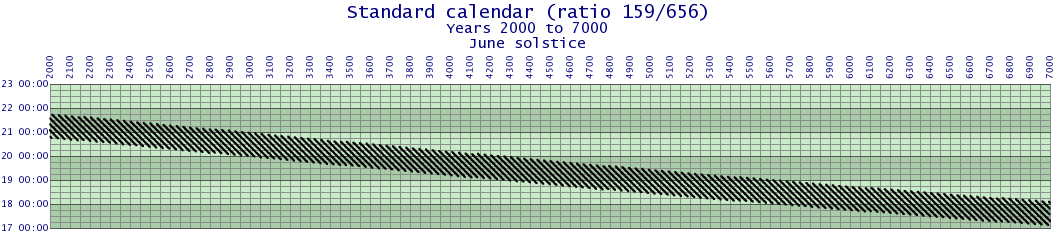
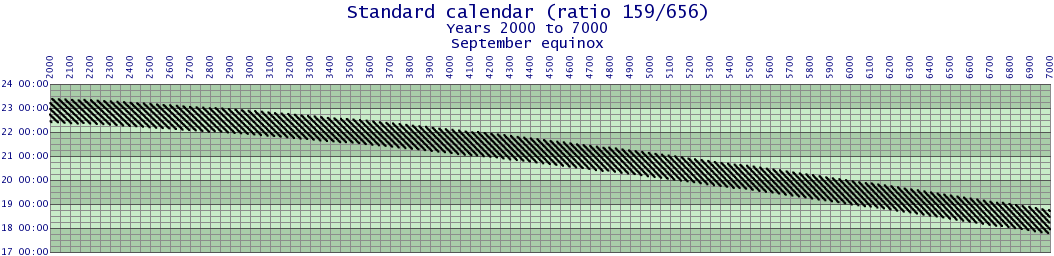


The Standard Calendar is tied to the March equinox. The tying of the calendar to the March equinox increases the error range for the September equinox and both solsitices.
The length of the day on Earth is not constant. Tidal braking from the Moon and Sun is slowly lengthening the day at a rate of about 15 seconds per day per million years. In the short term, this will require a change to the intercalation rules, so that the calendar remains closely aligned with the seasons. The way this is done is to take the length of the year, express it as a continued fraction and choose an approximation by truncating the continued fraction after four or five terms.
For example, the Standard Calendar uses the continued fraction
365 + 1
4 + 1
7 + 1
1 + 1
18 + 1
1 or 365+1/(4 + 1/(7
+ 1/(1 + 1/(18 + 1⁄1)))) or
[365; 4, 7, 1, 18, 1], which reduces to 365159⁄656 (approximately 365.24237805, or 365 days 5 hours 49 minutes 1.46341 seconds.)
The successive steps in the reduction of this continuing fraction are:
The 656-year cycle is composed of 19 cycles of eight leap years in 33 years followed by a cycle of seven leap years in 29 years.
The calendar will require different intercalation rules after about 3000 to 4000 years, when the March equinox starts to drift away from the nominal date of March 18 (Standard Calendar). The cycle of 8⁄33 has a length of about 0.24242424, and the 7⁄29 cycle has a length of about 0.24137931. Mixing these cycles in various combinations can give many good approximations between these two extremes. For example, the 31⁄128 cycle is made up of three cycles of 8⁄33 and one of 7⁄29.
The following table illustrates possible cycle lengths. It does not include cycle lengths for the calendar because these would need to be determined from future astronomical observations.
| Decimal | Time | Fraction | Subcycles |
|---|---|---|---|
| 365.24242424 | 365d 5h 49m 05.455s | 3658⁄33 | 8⁄33 × 1 |
| 365.24237805 | 365d 5h 49m 01.463s | 365159⁄656 | 8⁄33 × 19, 7⁄29 × 1 |
| 365.24233129 | 365d 5h 48m 57.423s | 36579⁄326 | 8⁄33 × 9, 7⁄29 × 1 |
| 365.24229074 | 365d 5h 48m 53.921s | 36555⁄227 | 8⁄33 × 6, 7⁄29 × 1 |
| 365.24223602 | 365d 5h 48m 49.193s | 36539⁄161 | 8⁄33 × 4, 7⁄29 × 1 |
| 365.2421875 | 365d 5h 48m 45.000s | 36531⁄128 | 8⁄33 × 3, 7⁄29 × 1 |
| 365.24213836 | 365d 5h 48m 40.755s | 36577⁄318 | 8⁄33 × 7, 7⁄29 × 3 |
| 365.24210526 | 365d 5h 48m 37.895s | 36523⁄95 | 8⁄33 × 2, 7⁄29 × 1 |
| 365.24203822 | 365d 5h 48m 32.102s | 36538⁄157 | 8⁄33 × 3, 7⁄29 × 2 |
| 365.24199288 | 365d 5h 48m 28.185s | 36568⁄281 | 8⁄33 × 5, 7⁄29 × 4 |
| 365.24193548 | 365d 5h 48m 23.226s | 36515⁄62 | 8⁄33 × 1, 7⁄29 × 1 |
Eventually the year length will reach 3657⁄29 days (365 days 5 hours 47 minutes 35.172 seconds). After this time, the 6⁄25 cycle will come into play for fractional approximations.
In the longer term (millions of years), the calendar will eventually require changes to the lengths of the months. The length of each month is not constant but can be changed subject to the need to distribute the extra days as evenly as possible. The intercalary day is always to be placed at the end of the year. The number of days that have elapsed in the year to the end of a given month may be found by dividing the number of days in a leap year (or long year) by 12, multiplying by the month number and rounding down. The extra days are then allocated as evenly as possible through the year.
The 366-day year is an exception to these rules and is intended to reflect the month lengths of the Gregorian calendar as closely as possible while also making the month lengths more evenly distributed.
For year lengths of 365 days or less, this method gives the following results:
| Length | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 364 | 365 | 305⁄12 | 6010⁄12 | 913⁄12 | 1218⁄12 | 1521⁄12 | 1826⁄12 | 21211⁄12 | 2434⁄12 | 2739⁄12 | 3042⁄12 | 3347⁄12 | 365 | |
| 30 | 30 | 31 | 30 | 31 | 30 | 30 | 31 | 30 | 31 | 30 | 30/31 | |||
| 363 | 364 | 304⁄12 | 608⁄12 | 91 | 1214⁄12 | 1518⁄12 | 182 | 2124⁄12 | 2428⁄12 | 273 | 3034⁄12 | 3338⁄12 | 364 | |
| 30 | 30 | 31 | 30 | 30 | 31 | 30 | 30 | 31 | 30 | 30 | 30/31 | |||
| 362 | 363 | 303⁄12 | 606⁄12 | 909⁄12 | 121 | 1513⁄12 | 1816⁄12 | 2119⁄12 | 242 | 2723⁄12 | 3026⁄12 | 3329⁄12 | 363 | |
| 30 | 30 | 30 | 31 | 30 | 30 | 30 | 31 | 30 | 30 | 30 | 30/31 | |||
| 361 | 362 | 302⁄12 | 604⁄12 | 906⁄12 | 1208⁄12 | 15010⁄12 | 181 | 2112⁄12 | 2414⁄12 | 2716⁄12 | 3018⁄12 | 33110⁄12 | 362 | |
| 30 | 30 | 30 | 30 | 30 | 31 | 30 | 30 | 30 | 30 | 30 | 30/31 | |||
| 360 | 361 | 301⁄12 | 602⁄12 | 903⁄12 | 1204⁄12 | 1505⁄12 | 1806⁄12 | 2107⁄12 | 2408⁄12 | 2709⁄12 | 30010⁄12 | 33011⁄12 | 361 | |
| 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30/31 | |||
Compare the month lengths for the 365-day calendar with the 366-day calendar:
| Length | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 365 | 366 | 31 | 30 | 31 | 30 | 31 | 30 | 30 | 31 | 30 | 31 | 30 | 30/31 |
| 364 | 365 | 30 | 30 | 31 | 30 | 31 | 30 | 30 | 31 | 30 | 31 | 30 | 30/31 |
The length of the months for a 365-day year are the same as the lengths for the 366-day year except January has 30 days in the 365-day calendar. Thus, in the future it is easy to adjust the month lengths to make the year one day shorter by subtracting one day from the month of January, and the remaining 31-day months are evenly distributed. Further adjustments will require changes to several months to ensure the 31-day months are as evenly distributed as possible.
An alternative schedule is presented below in Table 6. It is based on the schedule in Table 4 but is designed so that the length of only one month is changed at a time and no month is ever lengthened.
| Length | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Shortened Month | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 365 | 366 | 31 | 30 | 31 | 30 | 31 | 30 | 30 | 31 | 30 | 31 | 30 | 30/31 | — |
| 364 | 365 | 30 | 30 | 31 | 30 | 31 | 30 | 30 | 31 | 30 | 31 | 30 | 30/31 | January |
| 363 | 364 | 30 | 30 | 31 | 30 | 31 | 30 | 30 | 31 | 30 | 30 | 30 | 30/31 | October |
| 362 | 363 | 30 | 30 | 30 | 30 | 31 | 30 | 30 | 31 | 30 | 30 | 30 | 30/31 | March |
| 361 | 362 | 30 | 30 | 30 | 30 | 31 | 30 | 30 | 30 | 30 | 30 | 30 | 30/31 | August |
| 360 | 361 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30/31 | May |
| 359 | 360 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 29/30 | December |
Assuming the day lengthens by 15 seconds every million years, the year will have 360 days in about 85 million years. At this time the solar day will have a length of about 24 hours and 21 minutes.