An Alternative Method of Calculating Leap Years

Contents

1. Introduction
2. The Tropical Year
3. The Julian calendar
4. The Gregorian Calendar
1. Current Rules
2. Short-term errors in the in the Gregorian calendar
3. Possible future changes to the Gregorian calendar
5. Periodic omission of leap years
6. Other calendars
1. The Persian Calendar
2. The Hebrew Calendar
7. An Alternative Leap Year Rule
1. Example - Julian calendar
2. Example - Transition from the Gregorian calendar
3. Example - Replacing the Gregorian calendar with a leap-week calendar
4. Example - A Calendar for Mars (Leap Days)
5. Example - A Calendar for Mars (Leap Weeks)
8. Further Reading

The Gregorian calendar was introduced in 1582 by Pope Gregory XIII. Since then, there have been many proposals for calendar reform. Most proposals for calendar reform have emphasised changing the layout of the calendar, but have largely left the determination of leap years alone on the assumption that the method for intercalating leap years was flawless. I disagree with this assumption because the Gregorian method for the intercalation of leap years is not as foolproof as people believe.

One example of the flaws inherent with the four-step Gregorian method of intercalation was revealed during the Y2K incident, during which it was discovered that many software applications were incorrectly marking the year 2000 as being a common year, or not a leap year. Such flaws would not be possible if we used a simpler method to intercalate leap years.

In this document I will describe the flaws of the Gregorian method more fully and demonstrate an alternative that has fewer rules and that has the desirable side effect of having less variation in the timing of equinoxes and solstices over medium-term timespans. The method described here is not a new idea because the Hebrew calendar uses similar rules for the determination of leap years. What is probably new is the introduction of a generalised formula for the determination of leap years.

The year is defined as the length of the tropical year, which is the length of time taken by the Sun to return to the same equinox or solstice. This measure was chosen because it keeps the year in step with the seasons.

The tropical year can be measured in relation to a particular equinox or solstice, or in relation to the average of all points on the ecliptic. These times are not exactly the same. The Earth moves at different speeds in its orbit at different times of the year, in accordance with Kepler's second law of planetary motion. The equinoxes and solstices move around in the Earth's orbit due to precession. When an equinox or solstice is close to perihelion, a tropical year measured on that point will be longer than average. Conversely, when an equinox or solstice is close to aphelion, a tropical year measured on that point will be shorter than average. The mean tropical year removes this difficulty by averaging the year as measured for all points on the ecliptic.

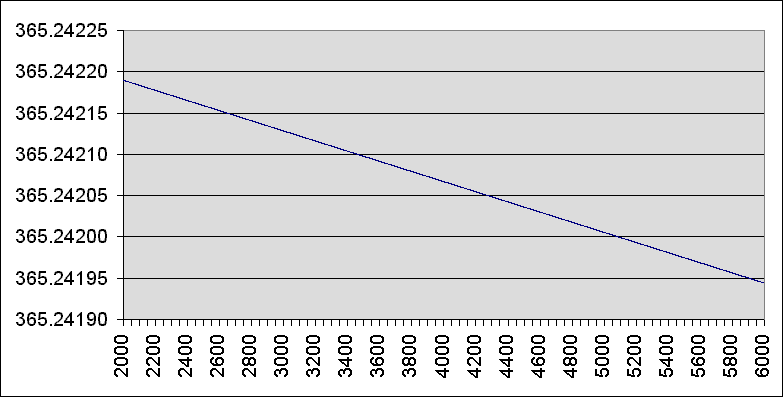
The length of the mean tropical year is not constant. The rotation of the Earth is gradually being slowed down due to tidal drag from the Moon and the Sun. This increases the length of the mean solar day, and causes the length of the mean tropical year to decrease by about 0.0000061 days per century, or about 0.53 seconds per century. A prediction for the decline is shown in the accompanying graph, where the length of the mean tropical year declines from about 365.24219 days in 2000 CE to about 365.24194 days in 6000 CE.

The exact length of the year is a matter of some debate among astronomers. The Gregorian calendar was probably measured in relation to the March equinox tropical year, especially because Kepler's laws of planetary motion had not yet been discovered when the Gregorian calendar was devised. Most modern astronomers prefer to use the mean tropical year as their measure of the tropical year because of its more consistent length.

In this document, the mean tropical year is used throughout because its length varies more regularly over timespans of thousands of years, and because no equinox or solstice is inherently more important than any other. The difference between the mean tropical year and March equinox tropical year adds up to about one day every 5,000 years.

The Julian calendar was introduced by Julius Caesar in 44 BCE as a part of his reforms to the Roman calendar. The Julian calendar is 365 days in length, with years divisible by 4 having a length of 366 days. The Julian calendar is still in use in the astronomical community for date calculation due to its simplicity for calculations, but ceased to be used in civil calendars in 1923 when Greece adopted the Gregorian calendar.

The Gregorian calendar was introduced by Pope Gregory XIII in 1582. The reforms omitted ten days from the calendar to bring the March equinox back to a nominal date of March 21, and amending the rules for the Julian calendar so that three leap days were omitted every 400 years.

Leap years in the Gregorian calendar are calculated using the following set of rules:

• If the year is not divisible by 4, then the year is a common year with 365 days.
• If the year is divisible by 4 but not 100, then the year is a leap year with 366 days.
• If the year is divisible by 100 but not 400, then the year is a common year with 365 days.
• If the year is divisible by 400, then the year is a leap year with 366 days.

These rules are fairly easy to use, because it is easy to determine if a number is divisible by 4, 100 or 400. However, the rules for determining leap years are not necessarily as easy to incorporate into computer software as they are to remember. One aspect of the Y2K episode was the use of incorrect leap year calculation rules in many software applications, which incorrectly declared 2000 CE to be a common year.

These rules give a year that is 365.2425 days long on average.

A problem with the Gregorian rules is that the rules do not provide smooth corrections to the calendar. Such events as the timing of the equinoxes and solstices can occur on as many as four different days in a 400-year span of the Gregorian calendar.

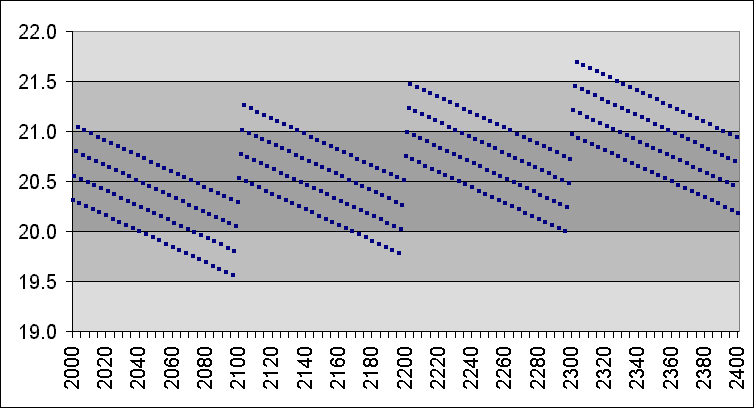
The illustration shows these errors for the March equinox, with the date and time plotted in Universal Time. Although the usual date quoted for the March equinox is March 21, the most common date for the March equinox is actually March 20 when measured from the Greenwich meridian. After 400 years, the cycle repeats approximately.

Sometimes the equinox falls on March 19 or March 21. The range of equinox dates in the 400 years shown in the illustration is about 53 hours. If timezones ahead of Universal Time are considered, it is possible for the equinox in these time zones to fall on March 22, while retaining some instances of the equinox on March 19.

A set of rules that spaces leap years more regularly would have smaller deviations.

Due to the changing length of the tropical year as expressed in days, the rules for determining leap years will need to be revised from time to time so as to keep the year in step with the seasons. The actual length of the mean tropical year is presently about 365.24219 days, so the Gregorian calendar is too long by about one day every 3200 years.

One possible rule would be to omit a leap year every 3200 years, so that 3200 CE is not a leap year. This leads to an average year length of 365.2421875, which is close to the current value of the tropical year of 365.24219 days. However, this rule suffers from the weakness that it does not account for the changing length of the tropical year. By the time 3200 arrives, the length of the tropical year will have decreased to about 365.24147 days, so the year should be omitted earlier.

To keep the year in step with the seasons for 5,000 years in the future, we could institute the following rules for leap years after 2000 CE:

• If the year is not divisible by 4, then the year is a common year with 365 days.
• If the year is divisible by 4 but not 100, then the year is a leap year with 366 days.
• If the year is divisible by 100 but not 500, then the year is a common year with 365 days.
• If the year is divisible by 500, then the year is a leap year with 366 days.

These rules make no change to leap years before 2400 CE, so this rule can be implemented any time between now and 2400 CE.

These revised rules give a year that is 365.2420 days long on average. Over the 4600 years between 2400 and 7000, two leap days are omitted.

After 7000 CE, further refinements to the calendar rules will be required. Such refinements will be required every 5000 years or so to keep the calendar in step with the seasons.

Now imagine it is 40,000 years into the future. There would be several spans of years each with its own set of rules that determine leap years, and the complete set of rules would not be easy to remember.

A possible set of rules after 40,000 years is given in the following table.

The problem with rules like this would be if it was necessary to keep track of them all. For example, astronomers or historians would find it difficult to count the exact number of days between arbitary dates in the civil calendar. This problem would be even worse if the year was measured in relation to a particular equinox or solstice, because the length of the tropical year as measured in relation to an equinox or solstice varies due to the precession of the Earth's orbit.

When the length of the mean tropical year drops below 365.24 days, there will be centuries where there are fewer than 24 leap years. Gregorian-like rules can no longer be applied easily because there is no obvious way to eliminate a second leap year in a century and yet retain the rule of century years not being leap years. Therefore, it will be necessary to abandon the century-year rule by this time.

Due to the potential complexity of rules over long periods of time, and the great error range over smaller periods of time, different methods of calculating the leap year should be considered.

The simplest alternative to the current leap year rules would be to omit one leap year in a regular period. At present, omitting one leap year every 128 years would be the most accurate method, giving an average year length of 365.2421875 days.

Because the length of the mean tropical year is decreasing, the 1 in 128 rule will also need to be altered over time. An overview of the rules is given in the following table.

These rules have the benefit of reducing the short term error by about 12 hours. The effect can be seen in the following illustration which illustrates a possible 128-year rule. The years 2048, 2176 and 2304 are not leap years.

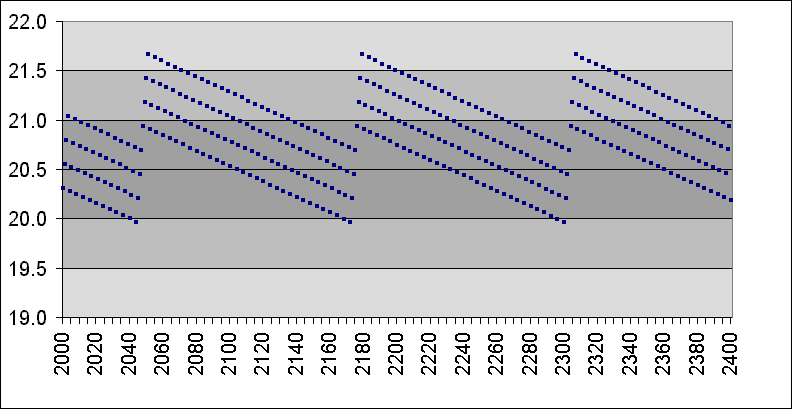
One drawback with this rule is the decreasing precision of intercalation as the omitted leap years get closer together. The difference between the omission of leap years every 128 years and every 124 years is only 0.000252 days per year, or about 22 seconds per year. The difference between the omission of leap years every 100 years and every 96 years is almost twice as great — 0.000417 days per year, or 36 seconds.

Can we do better? Let's consider the leap year rules that are employed in other calendars.

In Iran, the Persian calendar is in use. The Persian calendar, also known as the Iranian calendar, is a calendar with 12 months of 29, 30 or 31 days each, in years that are 365 or 366 days in length. It is an observation-based calendar, with the Persian new year beginning at the March equinox as observed from Teheran. The Persian calendar has leap years every four years, with the occasional leap year after five years instead of four. These five-year cycles occur about every 33 years. The Persian calendar has many cycles of 33-year cycles that are occasionally broken by 29-year and 37-year cycles.

The 33-year cycle has the benefit of reducing the maximum range of errors for the tropical year to much smaller values over time spans of centuries than the Gregorian calendar. It also greatly reduces the short term variation. In fact, the Persian calendar has the best possible match to the tropical year because the start of its year is determined by the timing of the March equinox.

The shortcomings of the Persian calendar are that the timing of the start of a new year is based on observation, not calculation. This means the calendar cannot be calculated out well in advance. Such a requirement is necessary for a general civil calendar that is intended to replace the Gregorian calendar. Its year is also measured in relation to the March equinox, and as such the length of the year will be subject to the periodic variations in length that are associated with the measurement of a year in relation to a particular equinox.

The Hebrew calendar is used by Jews all over the world for the timing of all religious holidays. The Hebrew calendar is a calculation-based lunisolar calendar. Using well-defined arithmetic, the calendar can be calculated precisely for hundreds of years in the future.

The Hebrew calendar uses an obsolete time unit called the helek (plural halakim). In English, this is usually translated as part. It is equal to 3+1/3 seconds, and there are 18 parts per minute.

In this discussion, we refer to days, hours, minutes and parts. To simplify the notation, we will abbreviate days as “d”, hours with “h”, minutes as “m” and parts as “p”.

The base of the Hebrew calendar is the mean lunar month. The mean lunar month is given a value of 29d 12h 44m 1p. The time the year is due to begin is called the molad. To calculate the molad, the number of lunar months that has elapsed is calculated, and a correctional term is added. The correctional term places the new moon in the correct time, and is equal to 3d 7h 38m 11p.

1. Find the number of months: MONTHS = FLOOR ( (235 × Hebrew Year + 13) / 19)
2. Multiply by the length of the lunar month: START = MONTHS × 29d 12h 44m 1p
3. Add the correctional term: START = START + 3d 7h 38m 11p

The algorithm is easier to calculate if all terms are reduced to parts.

1. Find the number of months: MONTHS = FLOOR ( (235 × Hebrew Year + 13) / 19)
2. Multiply by the length of the lunar month: START = MONTHS × 765433p
3. Add the correctional term: START = START + 86015p

After computing the start, it is used as the base for further computation.

In the Hebrew calendar, a particular Hebrew Year is a leap year if the remainder of (7 × Hebrew Year + 14) / 19 is less than 7.

To devise the proposed leap year rule, we combine the calculation-based elements of the Hebrew calendar with fractional terms that roughly replicate the leap year spacings of the Persian calendar.

To determine if a particular year is a leap year, we first define two values called Delta and Epsilon.

• Delta (Δ) is the length of the tropical year.
• Epsilon (ε) is a correctional or offset value that is a positive number less than Delta.

To compute the leap year, we multiply Delta by the year number, and then we add Epsilon to this result. We compare the digits after the decimal point of the result to Delta. If the digits after the decimal point are less than the digits after the decimal point of Delta, then the year is a leap year.

This method is too complex for general use, so we simplify it a little by replacing it with an algorithm that uses integers.

We define additional values:

• Cycle (C) is a suitable integer value. 100,000 can be used for ease of use, or smaller values that give a good approximation to the desired value.
• Remainder (R) is the result of the expression (Δ + ε) mod C.
• Quotient (Q) is the result of the expression (Δ + ε) div C where div is integer division. An equivalent way to derive Q is FLOOR((Δ + ε) / C).

Another way to express the same result is to ignore the digits before the decimal point, and treat Delta and Epsilon as two integer values between 0 and C – 1 inclusive. We multiply the year by Delta, add Epsilon, take the result mod C, and compare this Remainder to Delta. If the result is less than Delta, then the year is a leap year.

1. (Year × Δ + ε ) mod C = R
2. If R < Δ then the year is a leap year
3. The number of leap years until the end of the current year is equal to Q.

Compare this generic formula to the Hebrew leap year formula. (A Hebrew Year is a leap year if the remainder of (7 × Hebrew Year + 14) / 19 is less than 7.)

The value for Delta divided by Cycle is set to a good fractional approximation of the length of the mean tropical year over the period of time over which Delta is to remain valid, perhaps 1000 to 5000 years. Epsilon is carefully chosen so that the old leap year rule and the new leap year rule have as much overlap as possible. This overlap where both rules give the same results gives ample time to make the necessary changes to legislation, software and so forth. It should be possible to have an overlap of 20 years or more. The smaller the difference between the old values and the new values, the greater the overlap.

Determining the correct value for Delta is fairly easy. Determining the correct value for Epsilon is more difficult. Trial and error will generally be needed to produce values that give the desired results. In the following examples, the method for determining suitable values for Epsilon will not always be given.

This method of computation gives other results that are useful.

• The quotient that results when the calculation is performed can be used to determine how many leap days lie between two dates. If one date is before the leap day in a leap year and one date is after the leap day in a leap year, add or subtract correctional values as needed.
• The remainder can be used as a guide as to when an equinox or solstice is due. Divide the Remainder by the Cycle. The larger the result, the later the equinox or solstice will be due. If the Cycle number is a power of 10, then it becomes quite easy to do the necessary calculations once the remainder is known.

The above formula is a generalisation of common methods of determining the intercalation frequency for a calendar that use odd fractions like 23/95 or 31/128 to approximate the year. The idea of using such fractions is not new, but I have not seen them reduced to a generalised formula anywhere.

UPDATE: I have since seen the formula derived independently on the The Symmetry454 Calendar home page.

The Julian calendar can be defined using this formula because the formula is a generalisation of the leap year rule for the Julian calendar.

• Delta (Δ) = 1.
• Epsilon (ε) = 0.
• Cycle (C) = 4.

We can then work out leap years as follows:

1. (Year × 1 + 0) mod 4 = R
2. If R < 1 then the year is a leap year

If the transition begins in 2012, when the new rule takes over from the old rule, the March equinox will fall on March 20 about 95% of the time in the next 400 years.

Suppose these leap year rules were to commence in 2012 CE and to be current until 6000 CE. The current value for the mean tropical year is 365.24219 days. However, the mean tropical year is decreasing, so we must choose a value that would give a more accurate average over the period 2012 CE to 6000 CE.

Suppose we predict the mean tropical year over the period 2012 CE to 6000 CE to be equal to 365.24206 days. Good values for Delta and Cycle would be 61/252 (61/252 = 0.242063).

What value do we need to choose for Epsilon? The first few leap years after 2012 under the current Gregorian rules are 2012, 2016, 2020, 2024, 2028 and 2032. A good way that works well here is to set the result of the calculation for the first Leap year to be equal to one less than the value of Delta. To make the first leap year equal to the value of Delta, the year before the leap year must have a value of one less than Cycle. Therefore, to set Epsilon, we multiply the value of the year before the first leap year by Delta, take the remainder after dividing by Cycle, and subtract this remainder from Cycle – 1. This result is the value of Epsilon. In our example, that would be 251 – ((2011 × 61) mod 252) = 52.

This method won't work for all values of Delta.

Now with Delta and Epsilon known, we can calculate the leap years as follows:

1. (Year × 61 + 52) mod 252 = R
2. If R < 61 then the year is a leap year

Those take a while to prepare, so in Table 3 are some we prepared earlier:

Epsilon was chosen carefully so that the leap years follow the same pattern as the Gregorian leap years until 2043. This gives a 31-year window during which the new leap year rules would be phased in.

The leap years follow the Gregorian pattern until 2043. 2044 is the first year where the Gregorian leap year rules and the new proposed rules disagree on whether the year is a leap year. The leap year that follows 2040 is 2045, not 2044. The four-year gap with the occasional five-year gap is a characteristic of the proposed method that it shares with the Persian calendar. By contrast, the Gregorian calendar has four-year and eight-year gaps, and this leads to a less accurate calendar.

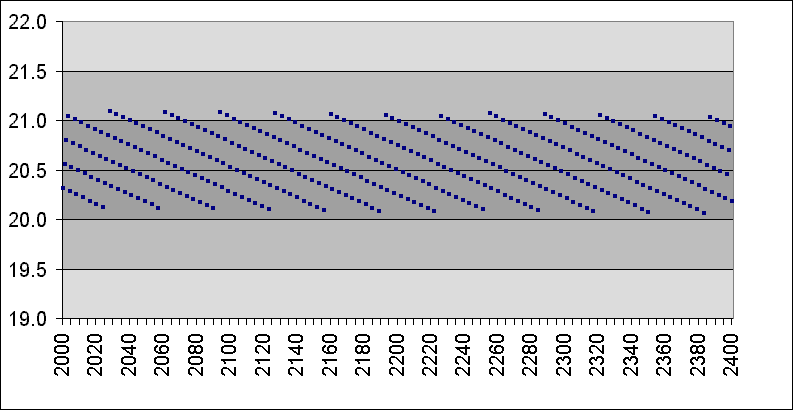
The accuracy of the calendar in tracking the mean March equinox is shown in the following illustration.

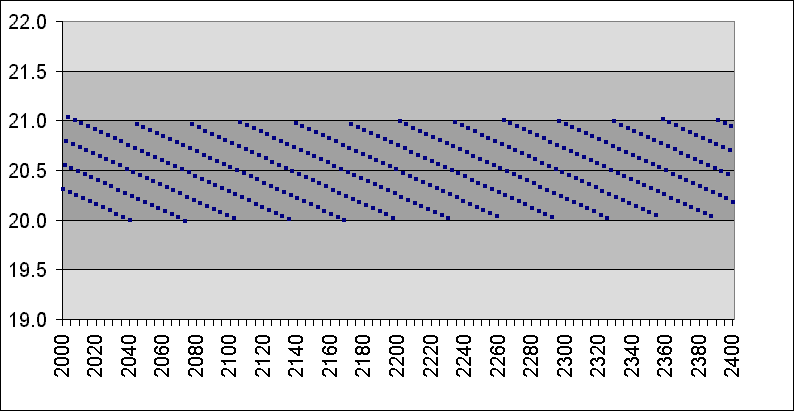
The actual March equinox will not track the calendar quite as precisely as shown in the illustration because the mean March equinox is shorter than the true March equinox. The March equinox tropical year is about 15 seconds longer than the mean tropical year, so over 400 years the March equinox will be about 1 hour and 40 minutes later. In addition, the timing of the true March equinox is subject to fluctuations that can make the equinox occur earlier or later by up to 15 minutes either side of the mean value.

If future calendar reform is more comprehensive, the Gregorian calendar could be replaced by a leap-week calendar. Such a calendar would have 52 weeks, and intercalate a whole week every 5 or 6 years instead of a single day every 4 or 5 years.

An example of a leap-week calendar is the Symmetry454 calendar. This calendar has 12 months in the year, February, May, August and November have five weeks (35 days), and the other eight months have four weeks (28 days). In years with leap weeks, December gets an extra week.

• More information: The Symmetry454 Calendar Home Page

Unlike leap-day calendars, the intercalation for leap-week calendars does not convert easily into an easy-to-remember rule. For a leap-week calendar, the surplus weeks per year is roughly 0.177456. This lies between the decimal expansions for 1/5 (0.200000) and 1/6 (0.166667). Because it is closer to the decimal expansion of 1/6, the better intercalation frequency is once every six years. That gives a year that is too short by almost two hours per year. After 92 years an extra week must be intercalated.

Because of the difficulty of finding a suitable match, the leap-week calendar would be a good candidate for this type of leap year determination.

A good fractional approximation for 0.177456 is 85/479 (0.177453), so Delta is 85 and Cycle is 479.

After some experimentation, we determine a value for Epsilon: 268. This value was chosen because it gives the same intercalation results as the Gregorian leap year rule for the years 2000 to 2047.

The first difference is in 2048. Gregorian-based rules for the leap year state that 2048 would be a leap year, but the remainder-based rule postpones the leap year to the following year.

The average length of a mean tropical year on Mars is 668.5921 Martian solar days. The fraction 0.5921 can be approximated by the fraction 45/76 (0.592105), so Delta is 45 and Cycle is 76.

1. (Year × 45 + 15) mod 76 = R
2. If R < 45 then the year is a leap year

The early Martian years would have the following pattern. Note that the first year is year zero.

The alternating 5-year cycle broken by an occasional 7-year cycle is characteristic of a Martian calendar calculated using this method. This occurs because the year fraction of 0.5921 lies between the decimal expansions for 3/5 (0.600000) and 4/7 (0.571429).

The average length of a Martian Mean Tropical Year is 668.5921 Martian solar days. To reduce the year to whole weeks, we divide this number by 7 and keep the remainder: 0.51315714. A good fractional approximation for this value is 39/76 (0.51315789). The denominator here is the same as the previous example, and the mathematical relationship between the two numbers is (45/76 – 1/2) = (39/76 – 1/2) × 7.

A good value for Epsilon is 0.

1. (Year × 39 + 0) mod 76 = R
2. If R < 39 then the year is a leap year

The early Martian years would have the following pattern:

This gives a very interesting pattern. Every second year is a long year. This pattern is only broken in the Martian year 39, where two long years occur consecutively. Because 38 Martian years is about equal to 71 Earth years, this discontinuity would happen only once or twice in a lifetime.

With a leap-week calendar, the two year lengths are 665 days and 672 days. A 672-day calendar would have 24 months of 28 days each. This symmetry is only broken in short years, where the last month of the year would have only 21 days.

A leap-week calendar for Mars that uses this system is described here.

• [ Hebrew Calendar Science and Myths ] – A good page that describes the calculation of the Hebrew calendar.
• [ The Symmetry454 Calendar ] – The home page for the proposed Symmetry454 calendar.